| Introduites par Osher & Sethian (1998), les courbes de niveaux sont des méthodes numériques permettant le calcul de la propagation spatiale d'un front au cours du temps. | |||||
|
>> Accueil << Les snakes Méthode des ballons Contours actifs géodésiques Les courbes de niveaux (level sets) |
Les courbes de niveaux (level sets)- haut de page - I - PrésentationOn définit le contour actif par une fonction du temps.jpg) définie
de définie
de 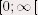 dans dans 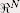 , où N est la dimension du
contour (dimension 2 pour des images 2D, dimension 3 pour des images 3D).
Le principe des courbes de niveaux est de représenter ce contour par une fonction , où N est la dimension du
contour (dimension 2 pour des images 2D, dimension 3 pour des images 3D).
Le principe des courbes de niveaux est de représenter ce contour par une fonction 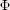 de dimension supérieure qui représente la distance signée des pixels (voxels en 3D) à cette courbe.
On considère la distance comme négative à l’intérieur de la surface, comme positive à l’extérieur.
Osher et Sethian ont mis en évidence l’équation qui en résulte :
de dimension supérieure qui représente la distance signée des pixels (voxels en 3D) à cette courbe.
On considère la distance comme négative à l’intérieur de la surface, comme positive à l’extérieur.
Osher et Sethian ont mis en évidence l’équation qui en résulte :
l’équation géométrique Euclidienne de chaleur : 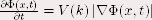 où x est un point de 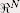 , t est le temps
et , t est le temps
et .jpg) est la vitesse à laquelle le contour se propage
(qui dépend du coefficient de courbure k de l’interface).
Tout dépend en fait de ce terme est la vitesse à laquelle le contour se propage
(qui dépend du coefficient de courbure k de l’interface).
Tout dépend en fait de ce terme 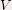 qui traduit l’attache aux données. qui traduit l’attache aux données.
On s’arrête lorsque 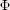 n’évolue plus,
c’est à dire lorsque n’évolue plus,
c’est à dire lorsque 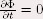
Dans le cas 2D, pour un temps donné  ,
la distance signée ,
la distance signée 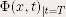 est une fonction à deux variables à
valeurs dans est une fonction à deux variables à
valeurs dans 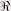 , dont la ligne de niveau zéro correspond en fait au contour actif. , dont la ligne de niveau zéro correspond en fait au contour actif.
Suivant cette approche, 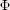 évolue dans le temps sous les
contraintes (forces) qui lui sont appliquées. évolue dans le temps sous les
contraintes (forces) qui lui sont appliquées.
En 3D, 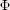 est une fonction à trois variables à valeurs
dans est une fonction à trois variables à valeurs
dans 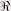 , et l’isoniveau est l’intersection
de , et l’isoniveau est l’intersection
de 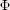 avec l’hyperplan de niveau zéro. avec l’hyperplan de niveau zéro.
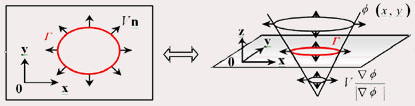
Les avantages de l’extraction du niveau zéro sont qu’elle permet de gérer automatiquement les changements de topologie et offre toujours une courbe (surface en 3D) fermée. 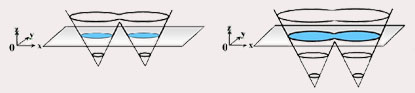
Les problèmes majeurs de cette méthode sont les difficultés d’implémentation. En effet, le calcul de la distance signée de la courbe de niveaux par rapport au contour actif et le calcul de son équation d’évolution au cours du temps ne sont pas simples. - haut de page - II - Résultats en images
|
||||