| Le principe des contours actifs est de faire évoluer un contour fermé initial vers une position d’équilibre, c’est-à-dire en direction des bords de l’objet à détecter. | |||||
|
>> Accueil << Les snakes Méthode des ballons Contours actifs géodésiques Les courbes de niveaux (level sets) |
Les contours actifs classiques : Les snakesSOMMAIREI - Présentation des snakesII - Méthode de résolutionA. Mise en place des équationsB. RésolutionIII - Avantages et InconvénientsA. Problèmes liés au paramétrageB. Problèmes liés à la topologieC. Problèmes liés aux calculsIV - Autres approches de résolutionA. Algorithme de GreedyB. Algorithme GVFV - Résultats en images- haut de page - I - Présentation des snakesLes contours actifs (ou snakes) ont été introduits par Kass et Witkin à la fin des années 80.C’est une méthode semi-interactive dont le principe consiste à placer dans l’image au voisinage de la forme à détecter un contour initial qui sera ensuite déformé sous l’action de plusieurs forces :  - haut de page - II - Méthode de résolutionA. Mise en place des équationsLe snake est une courbe paramétrée, où S est généralement l’abscisse curviligne (longueur de la courbe). Comme vu précédemment, l’utilisateur défini le contour initial 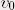 . Ensuite, la courbe évolue avec une certaine
vitesse. On cherche donc à déterminer cette vitesse telle que la courbe évolue vers un minimum local
correspondant aux contours des objets. . Ensuite, la courbe évolue avec une certaine
vitesse. On cherche donc à déterminer cette vitesse telle que la courbe évolue vers un minimum local
correspondant aux contours des objets.
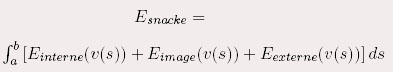
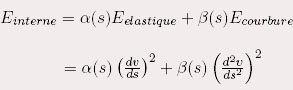  est le facteur d’élasticité et est le facteur d’élasticité et
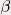 le facteur de rigidité du contour permettant
ainsi d’obtenir des courbes plus ou moins lisses. le facteur de rigidité du contour permettant
ainsi d’obtenir des courbes plus ou moins lisses.
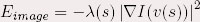 où le facteur 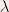 dépend de l’image dépend de l’image
 initiale et initiale et
 est l’opérateur gradient. On peut faire précéder
le gradient d’un filtrage passe-bas de l’image permettant d’obtenir des contours moins bruités et
d’augmenter leur zone d’influence. est l’opérateur gradient. On peut faire précéder
le gradient d’un filtrage passe-bas de l’image permettant d’obtenir des contours moins bruités et
d’augmenter leur zone d’influence.
S’il n’y a pas de contraintes extérieures, on peut alors écrire :  B. RésolutionOn note :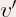 et et 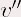 les dérivées
premières et secondes de les dérivées
premières et secondes de 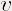 le long de la courbe et le long de la courbe et
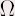 la région, l’énergie à minimiser est donc donnée par : la région, l’énergie à minimiser est donc donnée par :
 Pour minimiser cette énergie, on peut utiliser les équations d’Euler : on cherche alors à résoudre l’équation d’Euler suivante : (en considérant les coefficients  , ,
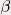 et et 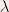 constants) : constants) :
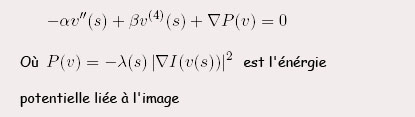 Afin de simplifier l’écriture, on pose 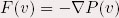 . .
L’équation de l’énergie à minimiser (avec  et et 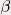 constants)
devient donc : constants)
devient donc :
 Les dérivées de l’équation sont ensuite approximées par des différences finies. On les met alors sous forme matricielle, nous donnant ainsi le schéma d’évolution suivant : 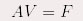  et et
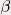
 Ce schéma aboutit à l’équation :  soit :   est la matrice identité de taille n X n et est la matrice identité de taille n X n et
 le pas du temps qui contrôle la vitesse de déplacement du snake.
On déduit la position à l’itération t en fonction des forces liées à l’image et de la position t-1. le pas du temps qui contrôle la vitesse de déplacement du snake.
On déduit la position à l’itération t en fonction des forces liées à l’image et de la position t-1.
Lorsque .jpg) et et
.jpg) sont très proches, on considère que la convergence
est réalisé et le processus s’arrête. sont très proches, on considère que la convergence
est réalisé et le processus s’arrête.
- haut de page - III. Avantages et InconvénientsCette formulation des snakes peut être utilisée dans de nombreuses applications telles que : la segmentation, la détection de contours ou d’arêtes, la stéréovision, le suivi spatio-temporel de formes...A. Problèmes liés au paramétrageLa définition de l’énergie dépend de la manière dont on paramètre le snake. De plus, le contour initial doit être suffisamment proche de l’objet pour pouvoir converger, sinon il risque de s’effondrer sur lui même.B. Problèmes liés à la topologieLe snake ainsi défini sera incapable de détecter distinctement deux objets sur une image : au mieux, les contours des deux objets seront liés. L’objet à détecter doit également être convexe, les snake ayant du mal à rentrer dans les concavités.C. Problèmes liés aux calculsLe calcul de la dérivée d’ordre 4 qui apparaît dans l’équation d’évolution pose des problèmes de discrétisation et d’instabilités numériques.- haut de page - IV - Autres approches de résolutionA. Algorithme de GreedyPour chaque point du contour actif,
la fonctionnelle d’énergie du contour actif,
la fonctionnelle d’énergie .jpg) est calculée pour tous
les points est calculée pour tous
les points 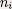 appartenant au voisinage
de appartenant au voisinage
de  .
Le point .
Le point 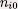 caractérisé par l’énergie
minimale caractérisé par l’énergie
minimale .jpg) est alors choisi pour
remplacer est alors choisi pour
remplacer  si si _E(vi).jpg) . .
Dans le cas contraire, le point de contour  n’est pas modifié.
Ce mécanisme est répété jusqu’à convergence (lorsque le contour obtenu à
l’itération n’est pas modifié.
Ce mécanisme est répété jusqu’à convergence (lorsque le contour obtenu à
l’itération  est identique celui obtenu l’itération
à est identique celui obtenu l’itération
à  ). ).
La déformation du contour dépend donc directement de la fonctionnelle d’énergie et non des équations d’Euler associées. B. Algorithme GVFC’est une méthode récente qui tente de limiter de manière plus ou moins satisfaisante les inconvénients du snacke classique tels que l’initialisation du snake et ses problèmes de convergence vers des régions de concavité.- haut de page - V - Résultats en images
|
||||