Extraction de contours et son extension du contour actif


			La recherche des contours dans une image numérique est un des problèmes les plus étudiés depuis l'origine des travaux sur l'imagerie numérique. Ceci est en grande partie dû à la nature très intuitive du contour qui apparaît très naturellement comme l'indice visuel idéal dans la plus grande partie des situations.
	>> Accueil << Définition et notions Méthode du gradient Estimation des contours Méthode du Laplacien Méthode de Canny et Deriche Exemple des différentes méthodes			Définition et notions SOMMAIRE I - Notion de contours A. Définition du contour B. Quelques exemples d'images II - Les filtres et masques A. Définition B. Utilisation des filtres C. Le filtrage linéaire d'une image - haut de page - I - Notion de contours A. Définition du contour Très schématiquement, les contours sont les lieux de variations significatives de l'information des niveaux de gris. L'image originale est représentée par son intensité lumineuse I(x,y) (par la suite on utilisera la notation f(x,y)). Les contours d'une image correspondent aux plus importantes variations de cette fonction intensité. On peut donc détecter les contours dans une image grâce à cette forte variation d’intensité entre deux zones proches. Les contours dans une image : 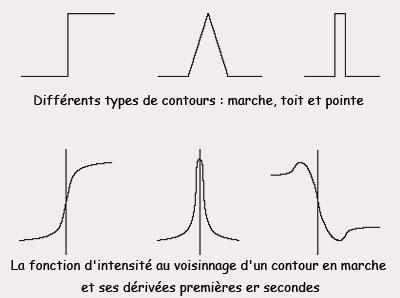Proviennent des discontinuités de la fonction de réflectance (texture, ombre) Proviennent des discontinuités de profondeur (bords de l'objet) Sont caractérisés par des discontinuités de la fonction d'intensité dans les images. Le principe de la détection de contours repose donc sur l'étude des dérivées de la fonction d'intensité dans l'image : les extrema locaux du gradient de la fonction d'intensité et les passages par zéro du laplacien. La difficulté réside dans la présence de bruit dans les images. B. Quelques exemples d'images La détection de contours à plusieurs domaines d'applications. Parmis eux on peut citer, l'imagerie médicale, la réalité virtuelle et le jeux vidéo, le traitement d'image, la cartographie... Voyons quelques exemples d'images ayant un rapport direct avec la détection de contours. Reconnaissance de formes et utilisation informatique Création de filtre et traitement d'images - haut de page - II - Les filtres et masques A. Définition L'utilisation de masque revient, mathématiquement, à filtrer l'image. On va donc réaliser un filtrage linéaire, dont les filtres sont obtenus à l'aide de masques appliqués sur des fenêtres de 2x2 ou 3x3 pixels. On note que la somme des coefficients de ces filtres est nulle (fonction de transfert nulle à la fréquence 0), et que les coefficients sont anti-symétriques. 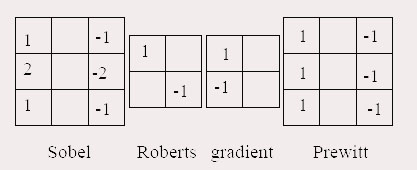B. Utilisation des filtres La réponse de l’un de ces filtres s’obtient de la façon suivante On place le pixel considéré dans le coin supérieur gauche de l'opérateur pour les fenêtres 2x2 et au centre pour les fenêtres 3x3. On multiplie la valeur de la fonction intensité par la valeur de l'opérateur pour les pixels voisins. On garde la valeur absolue de la somme. Cela donne une estimation de la dérivé partielle dans une direction (Ox) pour obtenir la dérivé partielle dans l'autre direction (Oy), on pivote le masque de 90° et on applique le même traitement. La norme de ce vecteur indique la force de la transition. Ces méthodes peuvent ensuite être combinées à un post-traitement adéquat comme le seuillage ou la fermeture des contours. C. Le filtrage linéaire d'une image Filtrer une image consiste à convoluer sa fonction d’intensité avec une fonction appelée réponse impulsionnelle du filtre. 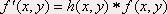Quelques formules sur les filtres: Dans le cas discret on obtient : (où H correspond à la dimension du masque de filtrage) 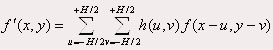Un filtre à réponse impulsionnelle h(x , y) séparable selon x et y est un filtre pour lequel : 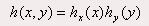Ce qui se traduit pour le filtrage d’une image par : 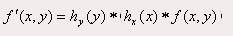Les principaux intérêts des filtres séparables sont : Ramener le problème du filtrage à un signal monodimensionnel. Réduire le temps de calcul. Possibilité d'implanter récursivement le filtre. - haut de page -