| Nous allons voir maintenant une approche qui a permis une bien meilleure compréhension des conditions d’une bonne détection de contours et qui a ainsi conduit à des détecteurs de très bonne qualité. | |||||||||
|
>> Accueil << Définition et notions Méthode du gradient Estimation des contours Méthode du Laplacien Méthode de Canny et Deriche Exemple des différentes méthodes |
Méthode du Laplacien- haut de page - I - Méthode de laplacienLa méthode du Laplacien est une méthode qui permet d'obtenir les contours par convolution. Le Laplacien utilise une matrice particulière pour la convolution, mais il existe d'autres opérateurs de dérivation comme ceux de Sobel ou de Roberts, qui permettent d'obtenir les contours avec d'autres matrices.Les opérateurs Laplacien ne sont pas directionnels. Si par hypothèse de départ, la fonction image est supposée continue, alors les propriétés de la dérivée seconde d'une fonction sont utilisées pour caractériser un contour par le passage à zéro de la dérivée seconde. Les opérations de détection de contours sont contraires aux méthodes de lissage, car elles consistent en une amplification des hautes fréquences spatiales qui met en évidence les transitions rapides. On peut les réaliser de diverses façons, notamment en utilisant les opérateurs de dérivation ou le Laplacien. On cherche donc à remplacer la recherche de maximas de la dérivée d’ordre 1 par le passage par zéro de la dérivée seconde. Ainsi, le contour se trouve là où le laplacien change de signe. 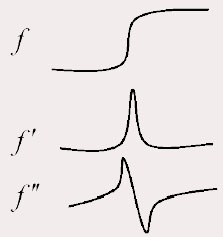 En 2D, le laplacien d’un image d’intensité 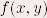 est défini par : est défini par :
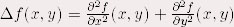 Approximation discrète possible : 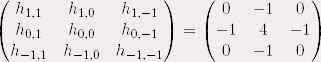

- haut de page -  |
||||||||

