| Le gradient est une grandeur vectorielle qui indique comment une grandeur physique varie en fonction de ses différents paramètres. Dans notre cas, nous voulons analyser la variation d’intensité entre chaque pixels de l’image | |||||
|
>> Accueil << Définition et notions Méthode du gradient Estimation des contours Méthode du Laplacien Méthode de Canny et Deriche Exemple des différentes méthodes |
Méthode du gradientSOMMAIREI - Le gradientA. DéfinitionB. Lien avec les contoursII - Propriétés du gradientA. Propriété 1B. Propriété 2III - Discrétisation du gradient- haut de page - I - Le gradientA. DéfinitionLe gradient est une grandeur vectorielle qui indique comment une grandeur physique varie en fonction de ses différents paramètres.La fonction de gradient en coordonnées cartésiennes se définit de la façon suivante :   B. Lien avec les contoursDans notre cas, nous voulons analyser la variation d’intensité entre chaque pixels de l’image.Intuitivement, le gradient indique la direction de la plus grande variation du champ scalaire, et l'intensité de cette variation. Par exemple, le gradient de l'altitude est dirigé selon la ligne de plus grande pente et sa norme augmente avec la pente. On peut donc considéré qu’un point de l’image (pixel) correspond à un maximum local de la norme du gradient. La normale du contour est donnée par le gradient. Si la valeur du gradient est non nulle on peut donc déduire que l’on se situe dans une zone de transition entre une partie claire et une partie sombre. 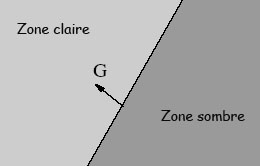 - haut de page - II - Propriété du gradientA. Propriété 1Le gradient est orthogonal aux courbes de niveaux de l’image.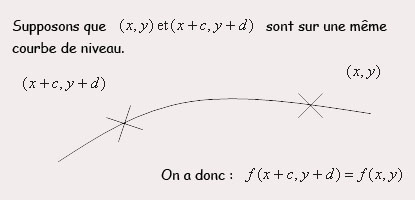  B. Propriété 2Le gradient est orienté dans la direction où le champ croit le plus localement, dans le sens de croissance du champ et cette puissance est d’autant plus forte que la norme du gradient est importante.
 Le champ est donc maximal lorsque l’on se situe dans la direction du gradient. On vérifie donc une première règle selon laquelle le champ, la variation, au voisinage de ( x , y ) , croit le plus dans la direction du gradient.
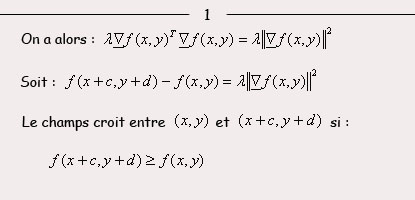 Le gradient est donc orienté dans le sens de croissance de f, c'est-à-dire depuis les faibles valeurs de f vers les fortes valeurs de f. Dans notre cas, le gradient croit de ( x , y ) vers ( x+c , y+d ).
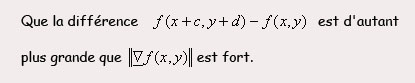 - haut de page - III. Discrétisation du gradientL’approximation des gradients horizontal et vertical revient à définir les maxima des gradient et donc à calculer les deux dérivées du gradient.Cependant, le gradient est une notion qui concerne des champs 2D différentiables et donc « analogiques ». Or, dans la pratique, on souhaite traiter des images numériques. Se pose alors le problème de savoir comment calculer un concept qui est théoriquement l'apanage des fonctions analogiques. Heureusement, chacune des composantes du gradient peut être approximée par filtrage numérique du champ échantillonné pourvu que le filtre soit choisi de manière appropriée. On peut ainsi définir les conditions que doit satisfaire la réponse impulsionnelle de ce filtre pour qu'on obtienne une approximation satisfaisante de l'opération de dérivation horizontale ou verticale. On effectuera la démonstration uniquement pour le gradient horizontal, puisque le gradient vertical s’obtient de façon identique. On s'intéresse donc ici à l'estimation locale du gradient horizontal et donc à la détection des contours verticaux dans l’image. Dans la pratique, on dispose de l’image échantillonnée, notée : 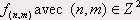
Supposons l’échantillonnage rectangulaire de pas L1 et L2. On a alors : 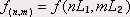 où f est le champ continu supposé différentiable où f est le champ continu supposé différentiable
En filtrant l’image initiale avec un filtre de réponse impulsionnelle finie, on pourra obtenir l’image des deux gradients. Le filtrage d’une image consiste à convoluer sa fonction d'intensité avec une fonction appelée réponse impulsionnelle du filtre selon la formule suivante :  Pour déterminer le filtre optimal 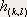 on doit : on doit :
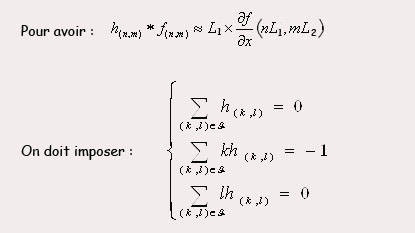
Le choix du filtre est donc sous-déterminé : on a une infinité de filtres solutions satisfaisant les conditions requises. D'où les choix multiples de filtres existant dans la littérature. - haut de page - |
||||